Elementary Graph Algorithms
Elementary Graph Algorithms
Representations of graphs
$$
G = (V, E)
$$
$G \to Graph, V \to Vertex, E \to Edge$, 式子说明图是由顶点和边这两个元素组成,那么只要把顶点和边表示出来,图就表示出来了。其中有两种方法,一种是邻接表表示,一种是用矩阵表示,根据不同的情景需要会选取不同的表示方法。
adjacency-list
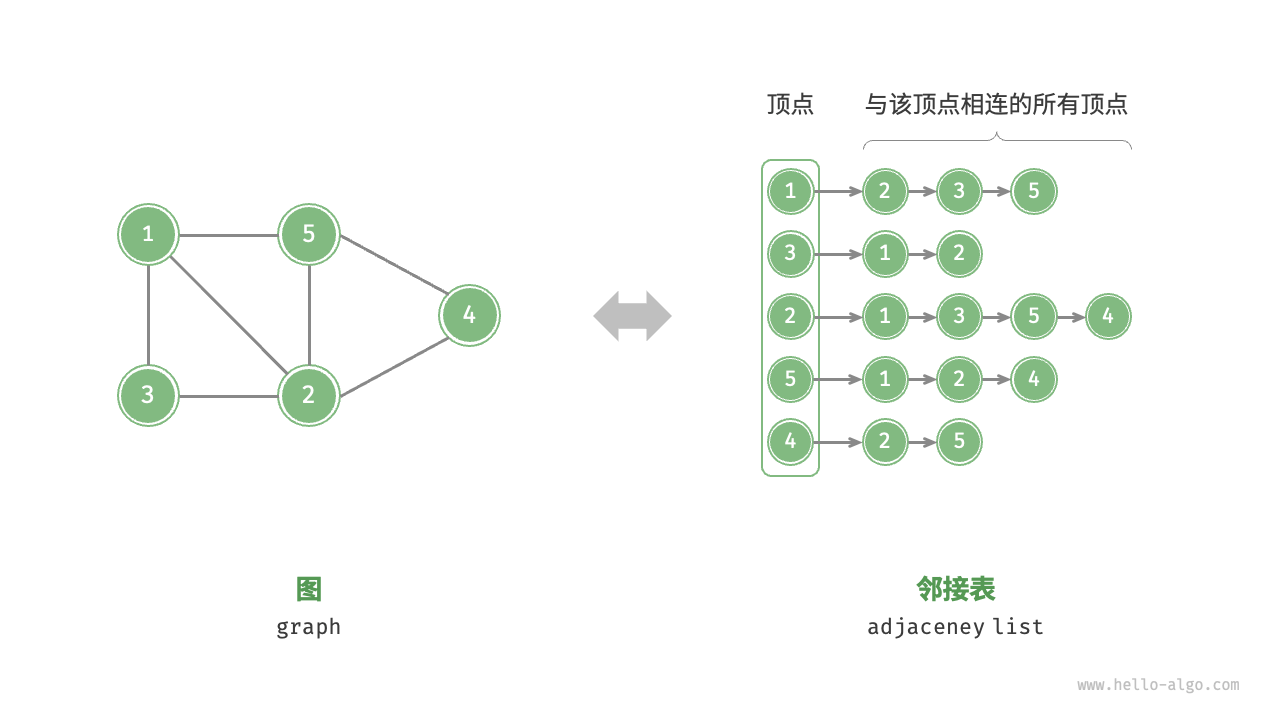
//邻接表可用链表,也可用哈希表
If $G$ is a directed graph, the sum of the lengths of all the adjacency lists is |E|.
If $G$ is an undirected graph, the sum of the lengths of all the adjacency lists is 2|E|.
1 | //下面是无向图的示例,有向图需要修改部分method代码 |
加权图
加权图即边是有权值的,可添加Edge类来实现
1 | class Edge { |
The adjacency-list representation is quite robust in that you can modify it to support many other graph variants.
//上方的代码顶点都是唯一的实例,还可以往其添加属性,这就体现了邻接表的灵活性,加上它的动态性以及内存效率等的优势,共同构建了其健壮性,使其能够支持很多其它的图变体。
邻接表查询边的存在性较慢, 邻接矩阵表示较快
adjacency-matrix
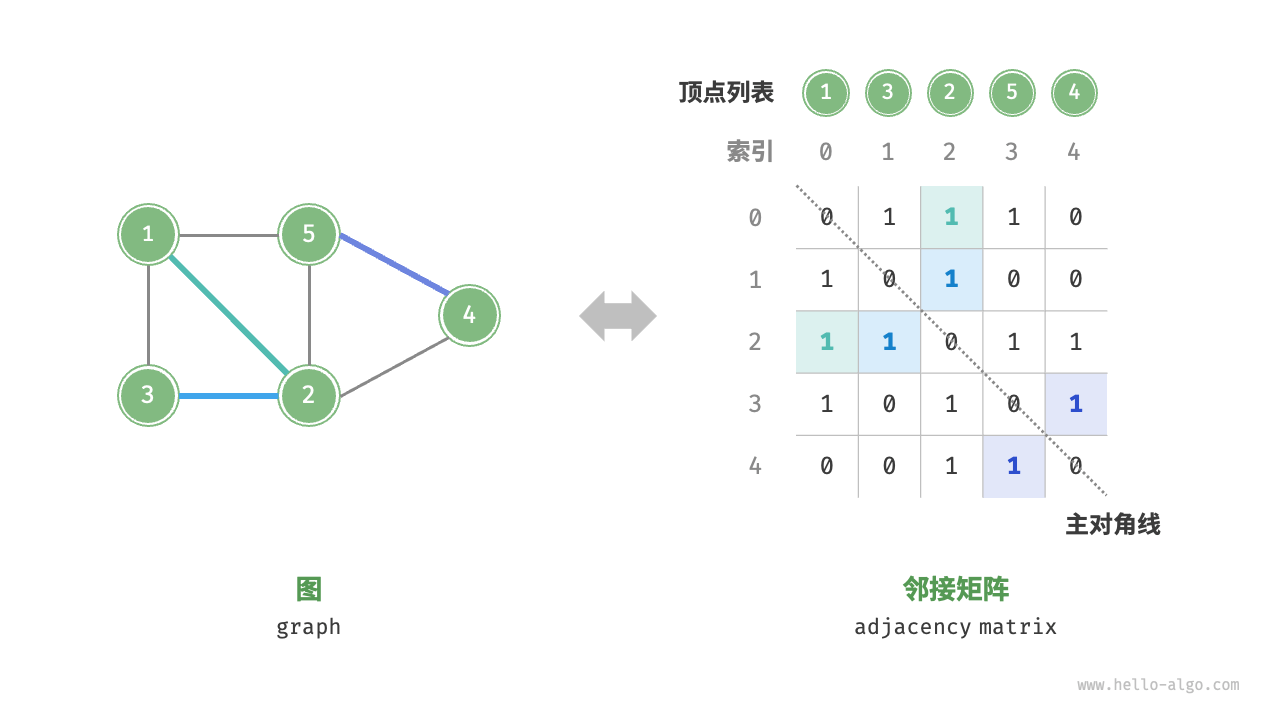
in an undirected graph, the adjacency matrix A of an undirected graph is its own transpose: $A = A^T$
//正是因为有这一性质,在一些应用中,只选择存储对角线以上的元素来提高内存效率。
1 |
|
邻接矩阵也可表示有权图,但空间浪费明显,无论稀疏还是密集:
在稀疏图中,尽管边的数量很少,但邻接矩阵仍然需要为每个可能的顶点对(即矩阵中的每个元素)分配空间。大多数这些顶点对之间实际上是没有边的,因此这些空间是浪费的。
在密集图中,虽然边的数量很多,但邻接矩阵仍然需要为每个顶点对分配空间,即使某些顶点对之间可能有多个边。例如,如果图中有两个顶点之间有5条边,邻接矩阵中的对应元素就需要存储这5条边的权重信息,而实际上只需要存储一个权重信息就足够了。
图规模较小时倾向于使用邻接矩阵
效率对比
| adjacency-matrix | adjacency-list(ll) | adjacency-list(hash) | |
|---|---|---|---|
| 边的存在性 | $O(1)$ | $O(E)$ | $O(1)$ |
| 添加边 | $O(1)$ | $O(1)$ | $O(1)$ |
| 删除边 | $O(1)$ | $O(E)$ | $O(1)$ |
| 添加顶点 | $O(V)$ | $O(1)$ | $O(1)$ |
| 删除顶点 | $O(V^2)$ | $O(V+E)$ | $O(V)$ |
| 内存空间占用 | $O(V^2)$ | $O(V+E)$ | $O(V+E)$ |
Exercises
题目是求基于邻接表表示的有向图,计算每个顶点的出度,入度的时间复杂度分别是多少。
顶点的出度很容易,每个顶点的邻接表存储的就是其指向的顶点,故直接计算每个顶点的邻接表
长度即为其出度,可知要遍历整个图,因此时间复杂度为O(V+E)。
顶点的入度的话,邻接表里存储的每个顶点都是被指向的顶点,也就是说在邻接表里的顶点每出现一次就表明其被指向一次,即入度+1,因此时间复杂度也为O(V+E)。
这题说的是有向图的转置,即把边的方向都反过来,描述计算$G^T$的算法。
伪代码如下
1 | function transposeAdjList(G): //时间复杂度:O(V+E) |
equivalent undirected graph等效无向图
大概就是保留原有向图所有顶点,边的方向被忽略,不包含任何自环
1 | function convertToUndirectedGraph(G): |
//这题提出了平方有向图的定义,就是边(u, v)在$G^2$中当且仅当在$G$中包含了$u \to v$ 不超过两条边的路径,换句话说,$G^2$ 包含了 $G$ 中所有顶点对之间长度不超过 2 的路径,要求描述计算$G^2$的算法。(原图中有自环的话平方图也会有,如果想排除自环就添加控制条件约束即可)
1 | //时间复杂度:O(|V|^2+|V|E). |
此题拓展:$G^k$ 包含了 $G$ 中所有顶点对之间长度不超过 $k$ 的路径
//这题说的是很多基于邻接矩阵的图算法都需要$\Omega (V^2)$的时间复杂度,但也有一些例外,比如查看一个有向图是否含有全局汇点(入度为|V| - 1,出度为0)。
1 | function findUniversalSink(G): |
这里确定候选汇点的形式很讲究,首先主对角线上元素都为0,因此无参考价值,故只在其上方查找。只要遇到一个1,就换到下一行(即下一个顶点),因为全局汇点没有出边,只要是0,就在该行一直往后验证。到这里可能就有疑问(其实就是我的疑问罢了):假设候选汇点一直都是1,那么就只检查了第一行,其它行都没检查呢,为啥只要这候选汇点不是真的全局汇点,整个图就没有全局汇点。其实每检查一条边就相当于检查了一个顶点,比如,如果$G[1][2] == 0$的话,就说明第二个顶点没有接受第一个顶点的入边,这同样是不符合全局汇点定义的,因为全局汇点是除了它自身,其它顶点都会指向它,因此该次检查排除了第二个顶点。如果$G[1][3]$也== 0的话,那就排除了第三个顶点,以此类推。所以无论$G[candidate][v]$等于0还是1,都是有价值的,这使得定位候选汇点是固定地检查|V| - 1遍即可。
这题说的是有向无环图的关联矩阵,直接建立顶点与每条边的对应关系,出边就是-1,入边就是1,没有关系就是0。题目要求描述$B B^T$矩阵的元素都代表什么。
- 对角线元素$c_{ii}$表示顶点 i 的度数,即与该顶点相关联的边的数量,包括入度和出度的边。
- 非对角线元素$c_{ij}$(其中 i≠j)表示顶点 i 和 j 之间共享的边的数量,经计算我们可以发现$B B^T$矩阵的元素要么是0,要么是负数,没有正数。所以如果 $c_{ij}=0$,则表示顶点 i 和 j 之间没有共享的边,而非零值则表示它们之间存在共享的边,如果是有多重边(multiple edges)的话,这个非零值就不只是-1了。这里没直接说多重图(multigraphs),是因为多重图是包括了自环和多重边的,但题目说的是有向无环图。
Breadth-first search
//时间复杂度:O(V + E)
$BFS(G, s)$
for each vertex u $\in G.V - {s}$ //初始化
u.color = WHITE
$u.d = \infty$ //d是距离
u.$\pi$ = NIL //$\pi$是前驱
s.color = $GRAY$
s.d = 0
s.$\pi$ = NIL
$Q = \not 0$ //初始化队列
ENQUEUE(Q, s)
while Q $\not = \not 0$
u = DEQUEUE(Q)
for each vertex v in $G$.Adj[u]
if v.color = WHITE
v.color = $GRAY$
v.d = u.d + 1
v.$\pi$ = u
ENQUEUE(Q, v) //可以发现队列里的顶点都是灰色的
u.color = BLACK
//图的广搜使用了颜色标记方法,白色表示顶点未被发现,灰色表示该顶点已被发现,但其邻接顶点可能还有未被发现的顶点,黑色则表示其邻接顶点全被发现。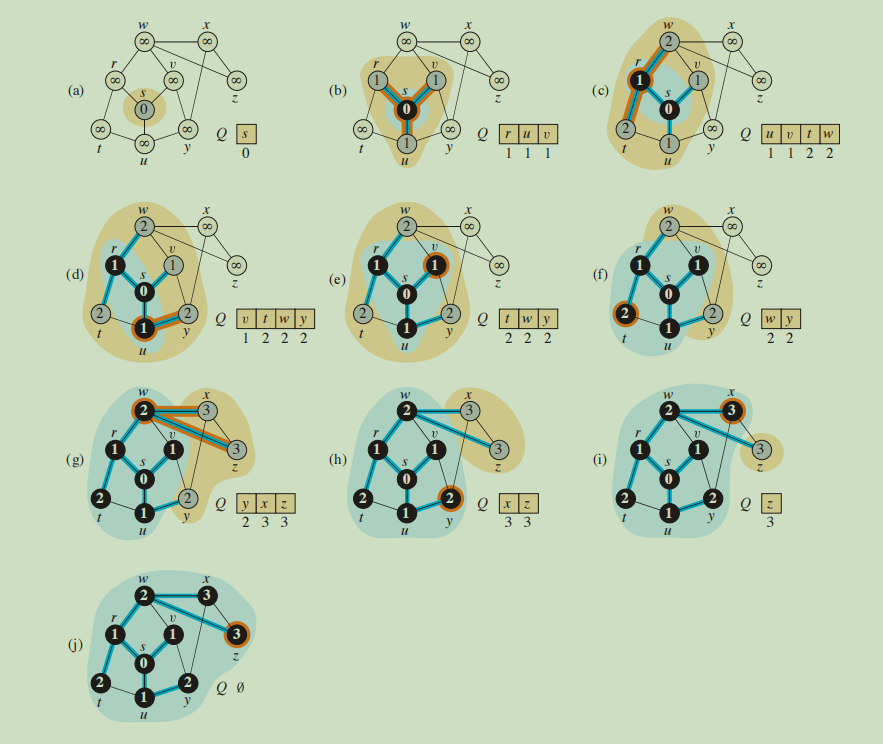
//该图展示了广搜全过程,广搜的结果可能不一样,这取决于for each vertex v in $G$.Adj[u]的遍历顺序。
Shortest paths
定义$\delta(s, v)$为从s到v的所有路径中的最少的边数
Lemma
(1) Let $G = (V, E)$ be a directed or undirected graph, and let $s \in V$ be an arbitrary
vertex. Then, for any edge $(u, v) \in E$,
$$
\delta(s, v) \leq \delta(s, u) + 1
$$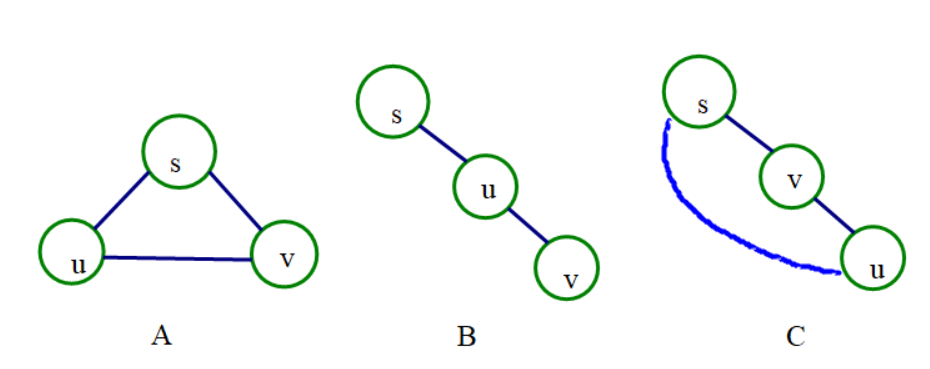
对于该引理有个方便记忆的描述,即三角形两边之和大于第三边,见A图,公式中的1就是(u, v)这条确定的边。
我一开始的想法是,(u, v)这条边有A, B, C三种情况(不严谨),A表示顶点u, v是同级的,对应$\delta(s, v) = \delta(s, u)$的情况;B表示顶点u相对于s的位置来说在v前面,对应$\delta(s, v) = \delta(s, u) + 1$的情况;C表示顶点v相对于s的位置来说在u前面,对应$\delta(s, v) < \delta(s, u)$的情况,特别地,C中的蓝色曲线代表了s到u的其他路径,所以说A是C的特殊情况,因此也可以分成两种情况,上面都是建立在u是从s可以到达的情况,不可以到达的情况参照下面的解释。
//上面纯属主观想法描述,可能存在纰漏以及说法不严谨的地方。CLRS里面的解释:
① 如果u是从s可以到达的顶点,那么v也是可达的,这种情况下从$s \to v$的最短路径不可能比从$s \to u$的最短路径再加上边(u, v)更长,因此不等式成立。//这是原话,看到这句我觉得我上面的想法貌似就是想表达这个意思。反正就是因为$\delta(s, u)$本身就是最短的,然后与顶点v再连一条边的话,那么$\delta(s, v)$的路径要么不经过u,要么经过u。不经过的话就必定有$\delta(s, v) \leq \delta(s, u) + 1$,因为如果不等号为>,那么$\delta(s, u) + 1$这条路径才应该是$\delta(s, v)$真正的路径,因为它更短;经过u的话就说明u是$\delta(s, v)$路径的一部分,此时在无向图中$\delta(s, v)$不仅有上限$\delta(s, u) + 1$,还有$\delta(s, u) - 1$这个下限。
② 如果u是从s不可以到达的顶点,那么在上面伪代码算法中可知,$\delta(s, u) = \infty$,等式显然成立。(2) Let $G = (V, E)$ be a directed or undirected graph, and suppose that BFS is run
on $G$ from a given source vertex $s \in V$ . Then, for each vertex $v \in V$ , the value v.d
computed by BFS satisfies $v.d \geq \delta (s, v)$ at all times, including at termination.
这里是用归纳法进行证明:归纳假设即为$v.d \geq \delta (s, v)$对于所有$v \in V$都成立
① 基本情况:在把源点s入队后,$s.d = 0 = \delta(s, s)$并且对于所有除s外的顶点v都有$v.d = \infty \geq \delta(s, v)$,因此等式成立。
② 归纳:考虑到一个白色顶点v是在对顶点u的邻接表搜索中被发现的,因此$v.d = u.d + 1$(可见伪代码),基于归纳假设,有$v.d \geq \delta(s, u) + 1$,由引理(1)可知$\delta(s, u) + 1 \geq \delta(s,v)$,因此等式成立。
- (3) Suppose that during the execution of BFS on a graph $G = (V, E)$, the queue Q
contains the vertices $<v_1, v_2, . . . , v_r>$, where $v_1$ is the head of Q and $v_r$ is the tail.
Then, $v_r.d \leq v_1.d + 1$ and $v_i.d \leq v_{i + 1}.d$ for i = 1, 2, . . . , r - 1.
这里也是用归纳法进行证明,但直接理解好像更容易。首先,假设队列里只能有不超过两种距离不同的顶点,如果是只有一种距离,假设为d,那么队列里肯定都是上一次出队的那个顶点(距离为d - 1)的邻接表(假设为u)里的,假设还没遍历完,那就继续添加,此时队列里顶点距离都是d。遍历完后就又要把当前队列第一个顶点出队,如果其邻接表为空,那就下一个继续出队操作,此时队列还是一种距离的情况,如果不为空,那就开始遍历其邻接表,只要是对邻接表u里面的元素执行出队,之后入队的顶点的距离都会是d+1,在此过程中距离就有两种情况,这种情况持续到u的所有顶点都出队了,那么此时队列里就只有d+1的顶点了,就又变回一种距离的情况了,以此类推,因此队列里不可能有超过两种距离,且从过程可知,跨度不超过1,因此$v_r.d \leq v_1.d + 1$ 成立,又因为代码中d的计算只有加没有减,因此在后面入队的肯定$\geq$在前面入队的,因此,$v_i.d \leq v_{i + 1}.d$ 也成立。
Corollary
- Suppose that vertices $v_i$ and $v_j$ are enqueued during the execution of BFS, and that $v_i$ is enqueued before $v_j$. Then $v_i.d \leq v_j.d$ at the time that $v_j$ is enqueued.
Theorem
- Let $G = (V, E)$ be a directed or undirected graph, and suppose that BFS is run
on $G$ from a given source vertex $s \in V$ . Then, during its execution, BFS discovers
every vertex $v \in V$ that is reachable from the source s, and upon termination,
$v.d = \delta (s, v)$ for all $v \in V$ . Moreover, for any vertex $v \not = s$ that is reachable from s, one of the shortest paths from s to v is a shortest path from s to $v.\pi$ followed by the edge $(v.\pi, v)$.
这里定理其实主要表达的就是$v.d = \delta (s, v)$,这就使得广搜可以用来求最短路径问题。
这个定理的证明采用反证法:
假设存在顶点的d值不等于它最短路径的距离。对于所有的这种顶点,设顶点v的最短距离为$\delta(s, v)$,通过引理(2)可知,$v.d \geq \delta(s, v)$,因此在这里的顶点v有$v.d > \delta(s, v)$①,当然不能有$v \not = s$,因为s.d = 0并且$\delta(s, s) = 0$。而且,顶点v必须是从s可达的,否则我们将有$\delta(s, v) = \infty \geq v.d$。设u是从s到v的最短路径上紧邻v前面的顶点(因为$v \not = s$,所以顶点u必须存在),这样就有$\delta(s, v) = \delta(s, u) + 1$②了。因此$\delta(s, u) < \delta(s, v)$,又因为我们设u的方式,所以有$u.d = \delta(s, u)$③。
结合①②③,就有了下图的公式,然后对v的所有情况进行讨论,推出矛盾,证明$v.d = \delta (s, v)$成立。具体看下图:
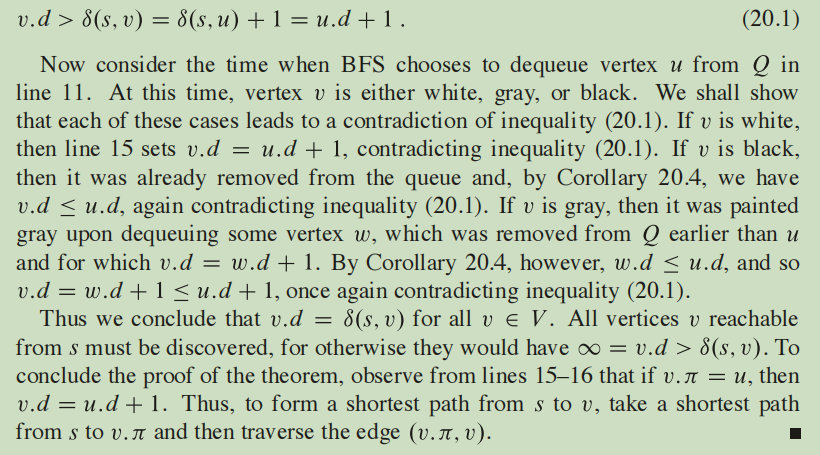
Breadth-first trees
上面广搜全过程图片中的蓝色边正展示了广度优先树在BFS过程中被建立,这个树对应着$\pi$属性。
形式化的定义即是:对于有源点s的图$G = (V, E)$,定义$G$的前驱子图(predecessor subgraph) $G_\pi = (V_\pi, E_\pi)$,其中$V_\pi = {v \in V: v.\pi \not = NIL} \cup {s}$,$E_\pi = {(v.\pi, v): v \in V_\pi - {s}}$。这样的$G_\pi$就是广度优先树,$E_\pi$为树边。
Depth-first search
- 与广搜不同,深搜的前驱子图可能包含多个树,因为深搜可能从多个源点进行。
它对$G_\pi$的定义是:$G_\pi = (V, E_\pi)$,其中$E_\pi = {(v.\pi, v): v \in V \wedge v.\pi \not = NIL}$。
深度优先搜索的前驱子图形成了包含多个深度优先树的深度优先森林。 - 深度优先搜索着色方法与广搜一样,该方法在这里保证了每个顶点只在一棵深度优先树中出现,因此这些树都是不相交的。
- 与广搜不一样的是,深搜过程还提供了时间戳,每个顶点有两个时间戳,第一个时间戳v.d记录了v什么时候第一次被发现,第二个时间戳v.f记录了什么时候完成了对v的邻接表的遍历。因为每个顶点都有两个时间戳,因此时间戳范围是$1 \to 2|V|$的整数,并且$v.d < v.f$。v在v.d之前为白色,在v.d到v.f之间为灰色,在v.f之后为黑色。下面是深搜伪代码:
//时间复杂度:O(V + E)
$DFS(G)$
for each vertex $u \in G.V$ //初始化
u.color = WHITE
u.$\pi$ = NIL
time = 0
for each vertex $u \in G.V$
if u.color == WHITE
DFS-VISIT $(G, u)$
DFS-VISIT $(G, u)$
time = time + 1
u.d = time
u.color =$GRAY$
for each vertex v in $G.Adj[u]$
if v.color == WHITE
v.$\pi$ = u
DFS-VISIT $(G, v)$ //体现了深度优先
time = time + 1
u.f = time
u.color = BLACK
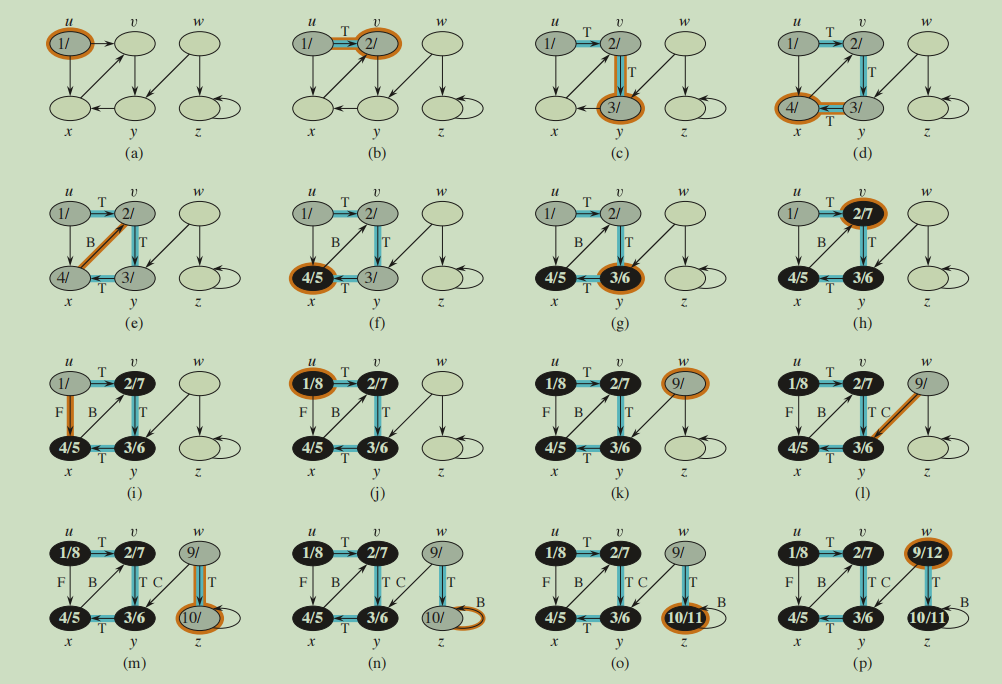
//这是深搜全过程图
Properties of depth-first search
- (1) 深度优先搜索生成的前驱子图$G_\pi$为一个有若干棵树的森林,因为深度优先树的结构与 DFS-VISIT 递归调用的结构完全对应,也就是说,$u = v.\pi$当且仅当 DFS-VISIT(G, v) 在搜索 u 的邻接表时被调用,此外,在深度优先森林中,顶点v是顶点u的后代当且仅当顶点v在顶点u为灰色的时间段里被发现。
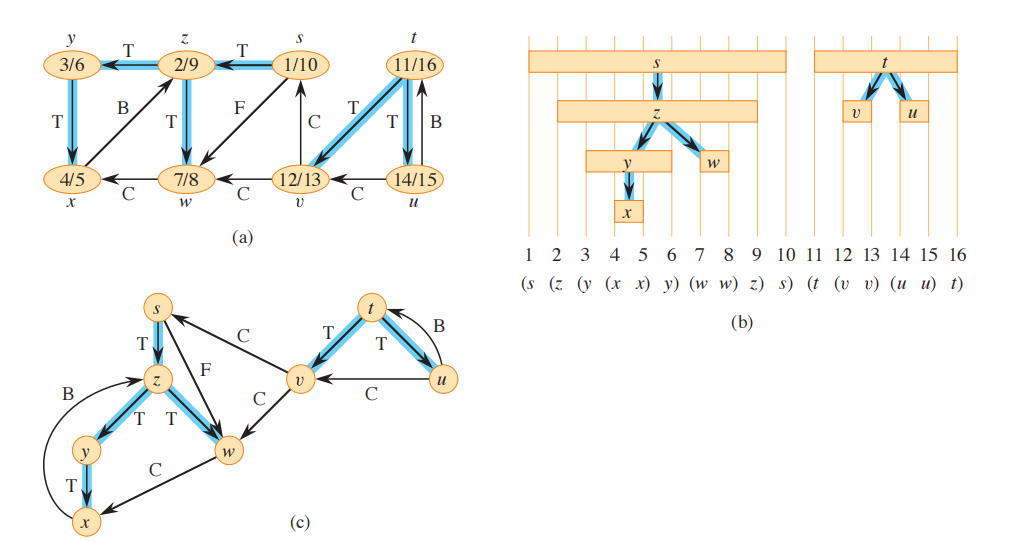
- (2) 顶点的发现时间和完成的时间具有括号化结构,与此对应的是括号化定理。
Parenthesis theorem
在对有向图或无向图 $G=(V, E)$的深度优先搜索中,对于任意两个顶点 u 和 v ,以下三种情况只有一种成立:
- 若 $[u.d, u.f]∩[v.d, v.f] = ∅$ ,则在深度优先森林中,u不是v的后代,v也不是u的后代。
- 若$[u.d, u.f]⊂[v.d, v.f]$,则在深度优先森林中,u是v的后代。
- 若$[v.d, v.f]⊂[u.d, u.f]$,则在深度优先森林中,v是u是后代。

Corollary(Nesting of descendants’ intervals)
在有向图或无向图$G = (V, E)$的深度优先森林中,顶点v是顶点u的真后代当且仅当$u.d < v.d < v.f < u.f$。
White-path theorem
在有向图或无向图$G=(V, E)$的深度优先森林中,顶点v是顶点u的后代当且仅当在搜索发现u的时刻u.d ,存在一条从u到v的全部由白色顶点构成的路径。
- $\Rightarrow$:如果v = u,那么从u到v路径上只有一个顶点u,当u.d = time时刻,u还是白色;如果v是u的真后代,根据推论,有$u.d < v.d$, 因此v是白色。由于v可以是u的任意后代,所以在深度优先森林中从u到v的唯一简单路径上的所有顶点在时间u.d时为白色。
- $\Leftarrow$:若在时刻u.d,存在一条从u到v的全部由白色顶点构成的路径,先假设在深度优先森林中v不是u的后代。不失一般性,假设路径上除v以外的每个顶点都成为u的后代。(否则,假设v是在没有成为u的后代的路径上离u最近的顶点。)设w是v在路径上的前驱,那么w就是u的后代(w和u实际上可能是同一个顶点)。由推论可知,$w.f \leq u.f$。又因为v必须在u被发现之后被发现,但在w完成的时间戳之前,则有$u.d < v.d < w.f \leq u.f$。根据括号化定理可知,$[v.d, v.f]⊂[u.d, u.f]$。由推论可知,v必须为u的后代
Classification of edges
- 树边(Tree edges):$G_\pi$上的边,若顶点v是通过边(u, v)第一次被发现,则(u, v)是一条树边。
- 后向边(Back edges):若边(u, v)为连接u和它在深度优先树中的一个祖先v的边,包括自环(即u = v),则(u, v)是一条后向边。
- 前向边(Forward edges):若边(u, v)为连接u和它的一个真后代v的非树边,则(u, v)是一条前向边。
- 横向边(Cross edges):其它所有边,它们可以连接同一深度优先树中的顶点,只要其中一个顶点不是另一个顶点的祖先;它们也可以连接不同深度优先树中的顶点。
Topological sort
对象是有向无环图(directed acyclic graphs),因此拓扑排序可以用来判断一个图有没有环,很多实际应用都需要使用有向无环图来指明时间的先后顺序。
拓扑排序是一种针对有向无环图(DAG)的排序算法,它不是基于元素之间的比较,而是基于它们之间的依赖关系。原理上,拓扑排序是对有向无环图进行深度优先搜索(DFS)或广度优先搜索(BFS)的一种应用。它通过这些搜索算法来确定图中节点的线性序列,这个序列满足:对于图中的每一条有向边(u, v)(从节点u指向节点v),u在序列中都出现在v之前。这样的序列满足了图中节点间的所有依赖关系。
- 依赖关系:
图中的每个节点代表一个任务或活动,有向边代表一个任务必须在另一个任务之后完成。拓扑排序能够确保对于任何节点,它的所有前驱节点(即所有指向它的节点)都在它之前被访问。伪代码:
TOPOLOGICAL-SORT$(G)$
call $DFS(G)$ to compute finish times v.f for each vertex v
as each vertex is finished, insert it onto the front of a linked list
return the linked list of vertices
Strongly connected components
- 有向图$G = (V, E)$的一个强连通分量是一个最大顶点集$C \subseteq V$,对于每一对顶点$u, v \in C$,那么u, v相互可达。
- $G 和 G^T$有完全相同的强连通分量。
- 分量图$G^{SCC} = (V^{SCC},E^{SCC})$,为简化后的有向图,把每个强连通分量压缩成一个顶点,以便研究它们之间的关系。
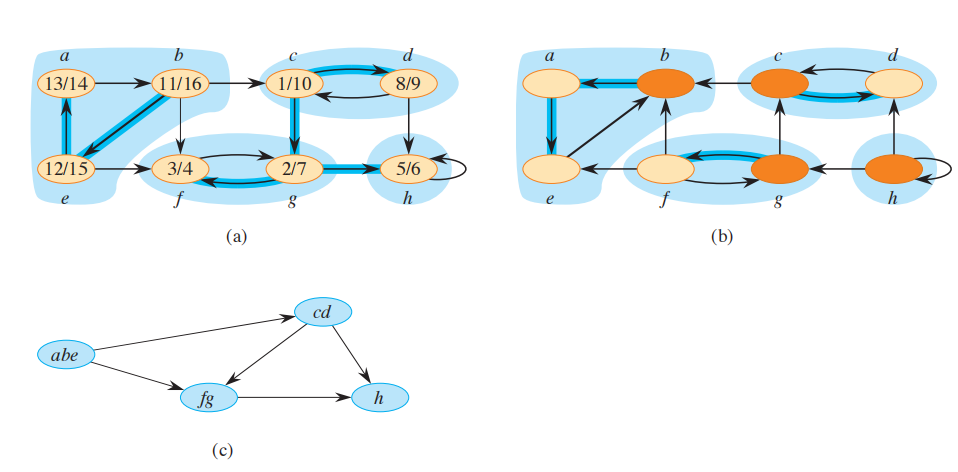
伪代码:
$STRONGLY-CONNECTED-COMPONENTS(G)$
1 call DFS(G) to compute finish times u.f for each vertex u
2 create $G^T$
3 call DFS($G^T$) , but in the main loop of DFS, consider the vertices
in order of decreasing u.f (as computed in line 1)
4 output the vertices of each tree in the depth-ûrst forest formed in line 3 as a
separate strongly connected component

