Minimum Spanning Trees
Minimum Spanning Trees
对于无向图$𝐺=(𝑉,𝐸)$,存在一个能够连接所有顶点的无环子集$𝑇⊆𝐸$,由于 𝑇 无环且连接所有顶点,因此 𝑇 一定为一棵树(树是特殊的图,为无环连通图),被称为生成树(spanning tree)。无向图$𝐺=(𝑉,𝐸)$的所有生成树都恰有$|𝑉|−1$条边。
设边$(𝑢,𝑣)∈𝐸$的权重为$𝑤(𝑢,𝑣)$,生成树权重为$𝑤(𝑇) = \sum_{(𝑢,𝑣)∈𝑇} 𝑤(𝑢,𝑣)$,所有生成树中权重最小的生成树被称为最小权重生成树(minimum-weight spanning tree),简称最小生成树(minimum spanning tree)。
Growing a minimum spanning tree
最小生成树问题的输入为一个无向连通图 $𝐺=(𝑉,𝐸)$, 伪代码如下:
$GENERIC-MST(G, w)$
1 $A = \not 0$
2 while A does not form a spanning tree
3 find an edge (u, v) that is safe for A
4 $A = A \cup {(u, v)}$
5 return A
能够被加入 𝐴 的边 (𝑢,𝑣) 被称为 𝐴 的安全边(safe edge)。通过 𝐴 维持了循环不变量可证明过程 GENERIC-MST 的正确性。在讨论如何识别安全边之前,我们需要了解一些定义。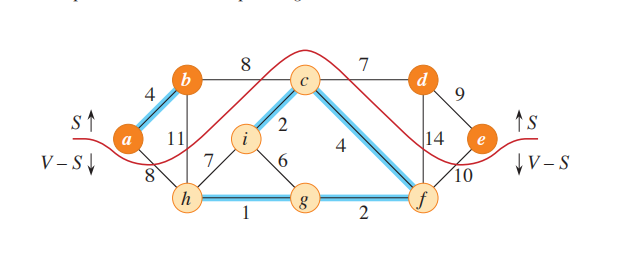
- $cut$:无向图$𝐺=(𝑉,𝐸)$的一个切割(cut) $(𝑆,𝑉−𝑆)$是对顶点𝑉的一个划分,分成两个区域
- $cross$:若边$(𝑢,𝑣)∈𝐸$的一个端点属于 𝑆 ,另一个端点属于𝑉−𝑆 ,则称边(𝑢,𝑣) 横跨(cross) cut (𝑆,𝑉−𝑆),看图的话就是跟红色分割线相交的边都是cross的边
- $respect$:若集合 𝐴 中不存在横跨切割 (𝑆,𝑉−𝑆) 的边,则称该切割不影响(respect) 𝐴
- $light\ edge$:权重最小的cross边即是轻量边(light edge)
原文如下:
当然最好还得知道树的性质:添加一条边就会构成环,删除一条边就会分裂成两棵树。
Theorem
设 𝐺=(𝑉, 𝐸) 为一个无向连通图,其权重函数为 𝑤: $𝐸\to𝑅$ ,设 𝐴⊆𝐸 ,且 𝐴 包含于 𝐺 的一棵最小生成树中。设 (𝑆, 𝑉−𝑆) 为 𝐺 中不影响 𝐴 的任意一个切割,若 (𝑢, 𝑣) 为横跨 (𝑆, 𝑉−𝑆) 的一条轻量边,则对于 𝐴 ,(𝑢, 𝑣) 是安全的。
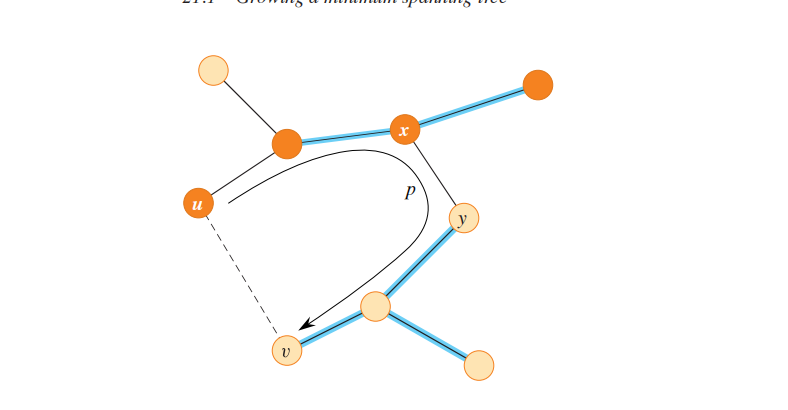
//图中橙色顶点属于S,其它顶点属于V-S,蓝色边就是A中的边
证明如下:
- 首先假设T是包含A的最小生成树,并假设T不包含轻量边(u, v),因为如果包含了,我们就不用证了。接着我们可以通过构造另一棵最小生成树T’,其中$A \cup {(u, v)} ⊆ T’$, 从而表明,边 (𝑢, 𝑣) 对于 𝐴 是安全的。
- 由图可知边(u, v)与$u \to v$的简单路径构成环路。因为u, v在cut(𝑆, 𝑉−𝑆)下分属两边,因此 𝑇 中至少有一条边属于简单路径 𝑝 并且横跨该切割,设 (𝑥, 𝑦) 为这样一条边。因为切割 (𝑆, 𝑉−𝑆) 不影响𝐴 ,所以 (𝑥, 𝑦) ∉ 𝐴。又因为边 (𝑥, 𝑦) 位于 𝑇 中从 𝑢 到 𝑣 的唯一的简单路径上,所以移除 (𝑥, 𝑦) 会导致 𝑇 分裂成两部分。此时添加 (𝑢, 𝑣) 将这两部分重新连接成一棵新的生成树 :𝑇′=(𝑇−{(𝑥,𝑦)})∪{(𝑢,𝑣)} 。
- 我们接下来要证明T’是最小生成树。由于 (𝑢, 𝑣) 为横跨 (𝑆, 𝑉−𝑆) 的一条轻量边且 (𝑥, 𝑦) 为横跨 (𝑆, 𝑉−𝑆) 的一条边,即 𝑤(𝑢, 𝑣)≤𝑤(𝑥, 𝑦) ,因此:
$w(T’) = w(T) - w(x, y) + w(u, v)$
$\leq w(T)$
但是 𝑇 为一棵最小生成树,有 𝑤(𝑇)≤𝑤(𝑇′) 。因此,有 𝑤(𝑇) = 𝑤(𝑇′) ,所以 𝑇′ 也是一棵最小生成树。 - 最后,我们还需要说明边 (𝑢, 𝑣) 对于 𝐴 是安全的。因为 𝐴⊆𝑇 且 (𝑥, 𝑦)∉𝐴 ,所以 𝐴⊆𝑇′ ,所以 (𝐴∪{(𝑢,𝑣)})⊆𝑇′ 。由于 𝑇′ 是一棵最小生成树,因此对于 𝐴 ,(𝑢, 𝑣) 是安全的。
感觉有点难咀嚼的话可以看看下面的另一种证明(算法4):
在算法执行的任何时候,图$G_A = (V, A)$是一个森林,$G_A$中每一个连通分量都是一棵树(一些树可能只包含一个顶点,例如在算法开始时,A是空的,因为还没开始加入安全边,并且此时森林包含了|V|棵树,每棵树都只有一个顶点)。此外,因为$A \cup {(u, v)}$必须是无环的,因此每一条安全边(u, v)都连接着$G_A$中的不同分量。
Corollary
设 𝐺=(𝑉, 𝐸) 为一个无向连通图,其权重函数为$𝑤:𝐸\to𝑅$,设 𝐴⊆𝐸 ,且 𝐴 包含于 𝐺 的一棵最小生成树中。设$𝐶=(𝑉_𝐶, 𝐸_𝐶)$为森林$𝐺_𝐴=(𝑉,𝐴)$中的一个连通分量(一棵树)。若 (𝑢,𝑣) 是连接 𝐶 和$𝐺_𝐴$中某一个其它的连通分量的一条轻量边,则对于 𝐴 ,(𝑢, 𝑣) 是安全边。
Proof:
切割$(V_C,V-V_C)$不影响A,又因为(u, v)是该切割的轻量边,因此,对于A,(u, v)是安全的。
The algorithms of Kruskal and Prim
这里描述的两种最小生成树算法详细介绍了上面的通用方法。它们各自使用一个特殊的规则来确定$GENERIC-MST(G, w)$的第3行中的find an edge (u, v) that is safe for A。在Kruskal算法中,集合A是一个森林,其顶点都是给定图的顶点。添加到A中的安全边总是图中连接两个不同分量的最低权重边。在Prim算法中,集合A形成了一棵树,算法执行过程中始终为一棵树。添加到A中的安全边始终是连接树和树中以外的顶点的最低权重边。下面的介绍中,两种算法都假设输入图是连通的,并由邻接列表表示。
Kruskal’s algorithm
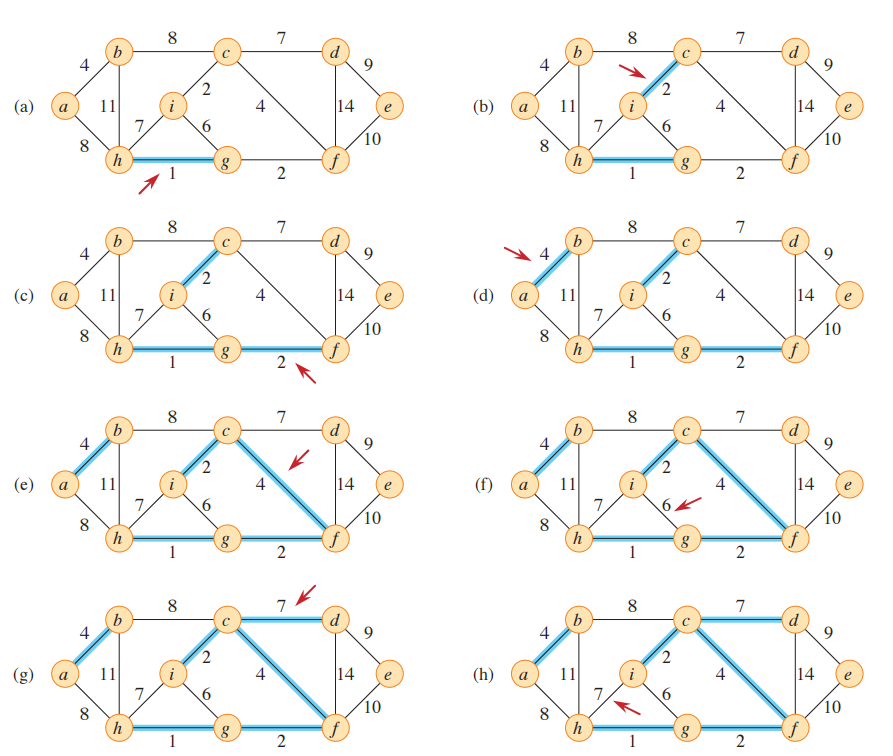
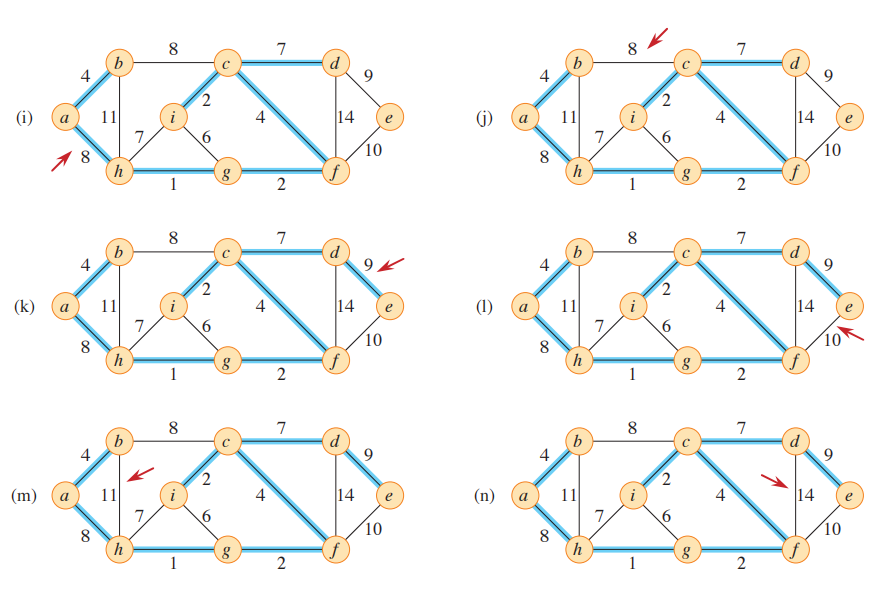
大家可以先通过上图感受一下该算法,蓝色边属于森林A,透过上图我们还可以观察到被添加到A中的安全边的权重是从小到大的,所以容易发现Kruskal算法是贪心算法,每次都加入权重最小的安全边,以此来保证总权重最小。该算法以按权重排序的顺序来考虑每条边,因此正在考虑的那条边已经是当前未加入生成树的边中的轻量边,只需再判断是否产生环而决定是否将它加入A,红色的箭头则指向在算法的每一步中所考虑的边。如果边(u, v)连接森林中两棵不同的树(注意单一的顶点也是树),则将其添加到森林中,从而合并两棵树。
- 设$C_1$和$C_2$表示由(u, v)连接的两棵树。因为(u, v)必须是连接$C_1$和其他树的轻量边,根据推论(Corollary), (𝑢, 𝑣) 是$𝐶_1$的一条安全边。
伪代码如下://时间复杂度:𝑂(𝐸 lg 𝑉)
$MST-KRUSKAL(G, w)$
1 A = $\not 0$ //初始化空集合
2 for each vertex $v \in G.V$
3 MAKE-SET(v) //使用并查集(disjoint-set)的数据结构来维护几个不相交的元素集, 每个集合都包含当前林的一棵树中的顶点,初始化即一个顶点一棵树
4 create a single list of the edges in G.E
5 sort the list of edges into monotonically increasing order by weight w
6 for each edge (u, v) taken from the sorted list in order
7 if FIND-SET(u) $\not =$ FIND-SET(v) //确定两个顶点是否属于同一棵树,同一棵树就会 成环
8 $A = A \cup {(u, v)}$ //把边(u, v)加入到A
9 UNION(u, v) //合并树
10 return A
上面说到了并查集数据结构,下面简要说一下,已掌握可跳过。
Disjoint-set
首先并查集用数组来实现,数组的值代表其父节点的位置,在上面代码中的初始化中,一个顶点就是一棵树,因此没有父节点,可以把所有顶点的数组值标为-1。
并查集支持两个操作:
- 查找(Find):确定某个元素属于哪个子集,它可以用来确定两个元素是否属于同一个子集。
- 合并(Union):将两个子集合并成一个集合
上面代码中的FIND-SET即是查找操作,对某个顶点i查找,即循环查找当前位置i的父节点,直到arr[i] = -1为止,返回i,如果两个顶点的FIND-SET返回结果一样,即两个顶点属于同一棵树。
合并操作即是先分别找到u,v的根节点,然后将其中一个根节点的父节点设为另一个顶点。这是最基础的并查集实现,要提高效率的话就要进行路径压缩和按秩合并。 - 路径压缩:在Find过程中在返回之前,路径中的顶点的父节点直接设为根节点,毕竟Find返回的就是根节点,这有利于下一次查询的效率。
- 按秩合并:上面所说的合并操作是将其中一个根节点的父节点设为另一个顶点,这未免有点随便。比如现在有一棵简单的树,一棵复杂的树,那么是将简单的往复杂的合并好还是复杂的往简单的合并好?答案是前者,如果把复杂的往简单的合并,那么原来在复杂树中的每个元素到根节点的距离都变长了,影响后面Find的效率;而如果把简单的往复杂的合并,到根节点距离变长的节点个数比较少。所以就引入秩,初始时每个顶点的秩设为1,那么什么时候秩会增加呢?这发生在合并时,如果两棵树深度相同,则新的根节点的秩+1。秩越高,树(或子树)就越复杂。
Prim’s algorithm
跟上面一样,我们可以先通过过程图感受一下: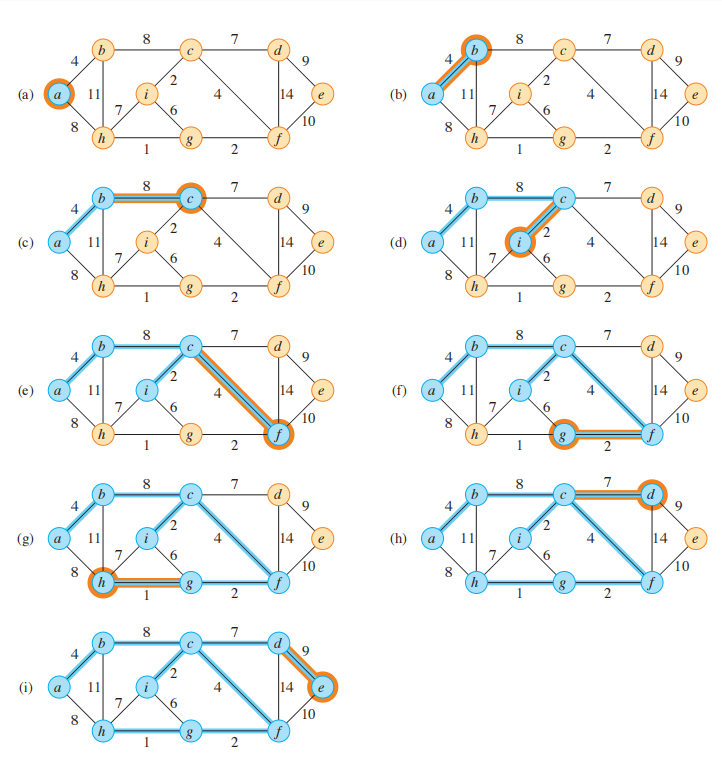
//从上图可以明显感受到与Kruskal算法不一样的是,蓝色边之间都是连通的,这里就揭露了Prim算法具有的一个性质是 𝐴 中的边总是构成一棵树,我们还可以发现添加边的权重是没有像Kruskal算法一样按权重排序的。
如图所示,这棵树以任意一个顶点 𝑟 为根节点,不断生长直到包含 𝑉 中所有顶点。每次加入到 𝐴 中的安全边永远是(𝐴, 𝑉−𝐴)切割的轻量边。根据Corollary,每次加入 𝐴 的边一定是安全边。该算法也满足贪心性质,因为在每一步它向树添加的一条边,都为树的权重贡献可能的最小量。
伪代码如下:
$MST-PRIM(G, w, r)$
1 for each vertex $u \in G.V$
2 $u.key = \infty$ // u.𝑘𝑒𝑦保存连接u和树中任一其它节点的所有边中最小的边的权 重,若不存在这样的边,即设为$\infty$,初始化时都设为$\infty$。
3 $u.\pi = NIL$ //u.𝜋 保存u在树中的父节点
4 $r.key = 0$ //把根节点r的key设为0,方便第9行第一个处理r
5 $Q = \not 0$ //创建基于 𝑘𝑒𝑦 属性的优先队列
6 for each vertex $u \in G.V$
7 INSERT (Q, u)
8 while $Q \not = \not 0$ //只要队列非空
9 u = EXTRACT-MIN(Q) //把u加到树(A)中
10 for each vertex v in $G.Adj[u]$ //更新u的非树邻居的key
11 if $v \in Q$ and w(u, v) < v.key
12 $v.\pi = u$
13 v.key = w(u, v)
14 DECREASE-KEY (Q, v, w(u, v)) //调整Q中v的key值
该算法保持以下三个循环不变量:
- $𝐴={(𝑣, 𝑣.𝜋): 𝑣∈𝑉−{𝑟}−𝑄}$,(算法终止时, 𝑄=∅,因此G的最小生成树$𝐴={(𝑣, 𝑣.𝜋): 𝑣∈𝑉−{𝑟}}$。)
- 已经放在最小生成树中的顶点都是V - Q中的顶点。
- 对于图中所有的顶点v∈Q,如果$v.\pi$不等于NIL,那么v.key小于正无穷大,v.key是连接v到已经放置在最小生成树中的某个顶点的轻量边$(v,v.\pi)$的权重。
Prim算法的运行时间取决于最小优先级队列Q的实现:
- 二叉堆:时间复杂度:$𝑂(𝐸lg𝑉)$
- 斐波那契堆:时间复杂度:$O(E+V lg V)$

